Portal:Mathematics

• 
  Abacus, a ancient hand-operated calculating.
• 
  Portrait of Emmy Noether, around 1900.
• 
  Euler's identity

Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). (Full article...)

Featured articles

• 

  

  Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

  
  
  In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
  
  In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
• 
  
  

  

  Portrait by Jakob Emanuel Handmann, 1753

  
  Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] ^ⓘ, Swiss Standard German: [ˈleɔnhard ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia.
  
  Euler is credited for popularizing the Greek letter $\pi$ (lowercase pi) to denote the ratio of a circle's circumference to its diameter, as well as first using the notation $f(x)$ for the value of a function, the letter $i$ to express the imaginary unit ${\sqrt {-1}}$, the Greek letter $\Sigma$ (capital sigma) to express summations, the Greek letter $\Delta$ (capital delta) for finite differences, and lowercase letters to represent the sides of a triangle while representing the angles as capital letters. He gave the current definition of the constant $e$, the base of the natural logarithm, now known as Euler's number. Euler made contributions to applied mathematics and engineering, such as his study of ships which helped navigation, his three volumes on optics contributed to the design of microscopes and telescopes, and he studied the bending of beams and the critical load of columns. (Full article...)
• 

  

  The manipulations of the Rubik's Cube form the Rubik's Cube group.

  
  In mathematics, a group is a set with an operation that satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.
  
  Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠$1$⁠ (these properties characterize the integers in a unique way). (Full article...)
• 
  
  

  

  The title page of a 1634 version of Hues' Tractatus de globis in the collection of the Biblioteca Nacional de Portugal

  
  Robert Hues (1553 – 24 May 1632) was an English mathematician and geographer. He attended St. Mary Hall at Oxford, and graduated in 1578. Hues became interested in geography and mathematics, and studied navigation at a school set up by Walter Raleigh. During a trip to Newfoundland, he made observations which caused him to doubt the accepted published values for variations of the compass. Between 1586 and 1588, Hues travelled with Thomas Cavendish on a circumnavigation of the globe, performing astronomical observations and taking the latitudes of places they visited. Beginning in August 1591, Hues and Cavendish again set out on another circumnavigation of the globe. During the voyage, Hues made astronomical observations in the South Atlantic, and continued his observations of the variation of the compass at various latitudes and at the Equator. Cavendish died on the journey in 1592, and Hues returned to England the following year.
  
  In 1594, Hues published his discoveries in the Latin work Tractatus de globis et eorum usu (Treatise on Globes and Their Use) which was written to explain the use of the terrestrial and celestial globes that had been made and published by Emery Molyneux in late 1592 or early 1593, and to encourage English sailors to use practical astronomical navigation. Hues' work subsequently went into at least 12 other printings in Dutch, English, French and Latin. (Full article...)
• 
  In classical mechanics, the Laplace–Runge–Lenz vector (LRL vector) is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
  
  The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)
• 

  

  Logic studies valid forms of inference like modus ponens.

  
  
  Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.
  
  Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
• 
  
  

  

  Portrait by August Köhler, c. 1910, after 1627 original

  
  Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ^ⓘ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.
  
  Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
  Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
• 

  

  High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

  
  
  General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.
  
  By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
• 
  
  

  

  Hilary Putnam

  
  The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.
  
  Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
• 
  
  

  

  Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

  
  Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
  
  Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
• 
  
  

  

  Kaczynski after his arrest in 1996

  
  Theodore John Kaczynski (/kəˈzɪnski/ ^ⓘ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ ^ⓘ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.
  
  Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's first and second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 
  
  

  

  Bust of Shen at the Beijing Ancient Observatory

  
  Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).
  
  In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
• 
  
  

  

  Cantor, c. 1910

  
  Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.
  
  Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)

Good articles

• 

  

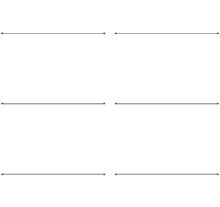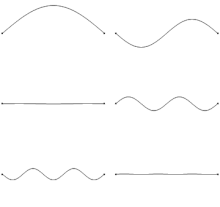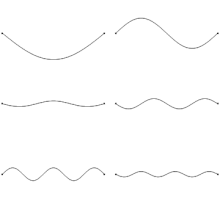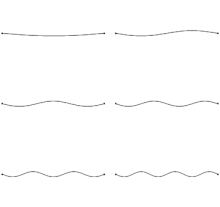
  The state of a vibrating string can be modeled as a point in a Hilbert space. The decomposition of a vibrating string into its vibrations in distinct overtones is given by the projection of the point onto the coordinate axes in the space.

  
  
  In mathematics, a Hilbert space (named for David Hilbert) generalizes the notion of Euclidean space. It extends the methods of linear algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions. A Hilbert space is a vector space equipped with an inner product operation, which allows lengths and angles to be defined. Furthermore, Hilbert spaces are complete, which means that there are enough limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space.
  
  Hilbert spaces were studied beginning in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the term Hilbert space for the abstract concept that underlies many of these diverse applications. The success of Hilbert space methods ushered in a very fruitful era for functional analysis. Apart from the classical Euclidean vector spaces, examples of Hilbert spaces include spaces of square-integrable functions, spaces of sequences, Sobolev spaces consisting of generalized functions, and Hardy spaces of holomorphic functions. (Full article...)
• 

  

  A Möbius strip made with paper and adhesive tape

  
  In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and August Ferdinand Möbius in 1858, but it had already appeared in Roman mosaics from the third century CE. The Möbius strip is a non-orientable surface, meaning that within it one cannot consistently distinguish clockwise from counterclockwise turns. Every non-orientable surface contains a Möbius strip.
  
  As an abstract topological space, the Möbius strip can be embedded into three-dimensional Euclidean space in many different ways: a clockwise half-twist is different from a counterclockwise half-twist, and it can also be embedded with odd numbers of twists greater than one, or with a knotted centerline. Any two embeddings with the same knot for the centerline and the same number and direction of twists are topologically equivalent. All of these embeddings have only one side, but when embedded in other spaces, the Möbius strip may have two sides. It has only a single boundary curve. (Full article...)
• 

  

  Graphical demonstration of the convergence of the sum 1/2 + 1/3 + 1/7 + 1/43 + ... to 1. Each row of k squares of side length 1/k has total area 1/k, and all the squares together exactly cover a larger square with area 1. Squares with side lengths 1/1807 or smaller are too small to see in the figure and are not shown.

  
  In number theory, Sylvester's sequence is an integer sequence in which each term is the product of the previous terms, plus one. Its first few terms are
  :2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443 (sequence A000058 in the OEIS).
  
  Sylvester's sequence is named after James Joseph Sylvester, who first investigated it in 1880. Its values grow doubly exponentially, and the sum of its reciprocals forms a series of unit fractions that converges to 1 more rapidly than any other series of unit fractions. The recurrence by which it is defined allows the numbers in the sequence to be factored more easily than other numbers of the same magnitude, but, due to the rapid growth of the sequence, complete prime factorizations are known only for a few of its terms. Values derived from this sequence have also been used to construct finite Egyptian fraction representations of 1, Sasakian Einstein manifolds, and hard instances for online algorithms. (Full article...)
• 

  

  Measuring the width of a Reuleaux triangle as the distance between parallel supporting lines. Because this distance does not depend on the direction of the lines, the Reuleaux triangle is a curve of constant width.

  
  In geometry, a curve of constant width is a simple closed curve in the plane whose width (the distance between parallel supporting lines) is the same in all directions. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler. Standard examples are the circle and the Reuleaux triangle. These curves can also be constructed using circular arcs centered at crossings of an arrangement of lines, as the involutes of certain curves, or by intersecting circles centered on a partial curve.
  
  Every body of constant width is a convex set, its boundary crossed at most twice by any line, and if the line crosses perpendicularly it does so at both crossings, separated by the width. By Barbier's theorem, the body's perimeter is exactly π times its width, but its area depends on its shape, with the Reuleaux triangle having the smallest possible area for its width and the circle the largest. Every superset of a body of constant width includes pairs of points that are farther apart than the width, and every curve of constant width includes at least six points of extreme curvature. Although the Reuleaux triangle is not smooth, curves of constant width can always be approximated arbitrarily closely by smooth curves of the same constant width. (Full article...)
• 
  Fermat's Last Tango is a 2000 off-Broadway musical about the proof of Fermat's Last Theorem, written by husband and wife Joshua Rosenblum (music, lyrics) and Joanne Sydney Lessner (book, lyrics). The musical presents a fictionalized version of the real life story of Andrew Wiles, and has been praised for the accuracy of the mathematical content. The original production at the York Theatre received mixed reviews, but the musical was well received by mathematical audiences. A video of the original production has been distributed by the Clay Mathematics Institute and shown at several mathematical conferences and similar occasions. The musical has also been translated into Portuguese. (Full article...)
• 

  

  The brute force algorithm finds a 4-clique in this 7-vertex graph (the complement of the 7-vertex path graph) by systematically checking all C(7,4) = 35 4-vertex subgraphs for completeness.

  
  
  In computer science, the clique problem is the computational problem of finding cliques (subsets of vertices, all adjacent to each other, also called complete subgraphs) in a graph. It has several different formulations depending on which cliques, and what information about the cliques, should be found. Common formulations of the clique problem include finding a maximum clique (a clique with the largest possible number of vertices), finding a maximum weight clique in a weighted graph, listing all maximal cliques (cliques that cannot be enlarged), and solving the decision problem of testing whether a graph contains a clique larger than a given size.
  
  The clique problem arises in the following real-world setting. Consider a social network, where the graph's vertices represent people, and the graph's edges represent mutual acquaintance. Then a clique represents a subset of people who all know each other, and algorithms for finding cliques can be used to discover these groups of mutual friends. Along with its applications in social networks, the clique problem also has many applications in bioinformatics, and computational chemistry. (Full article...)
• 
  In mathematics, the three-gap theorem, three-distance theorem, or Steinhaus conjecture states that if one places n points on a circle, at angles of θ, 2θ, 3θ, ... from the starting point, then there will be at most three distinct distances between pairs of points in adjacent positions around the circle. When there are three distances, the largest of the three always equals the sum of the other two. Unless θ is a rational multiple of π, there will also be at least two distinct distances.
  
  This result was conjectured by Hugo Steinhaus, and proved in the 1950s by Vera T. Sós, János Surányi, and Stanisław Świerczkowski; more proofs were added by others later. Applications of the three-gap theorem include the study of plant growth and musical tuning systems, and the theory of light reflection within a mirrored square. (Full article...)
• 

  

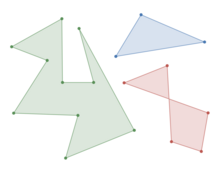
  Two simple polygons (green and blue) and a self-intersecting polygon (red, in the lower right, not simple)

  
  In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a piecewise-linear Jordan curve consisting of finitely many line segments. These polygons include as special cases the convex polygons, star-shaped polygons, and monotone polygons.
  
  The sum of external angles of a simple polygon is $2\pi$. Every simple polygon with $n$ sides can be triangulated by $n-3$ of its diagonals, and by the art gallery theorem its interior is visible from some $\lfloor n/3\rfloor$ of its vertices. (Full article...)
• 
  
  

  

  Francis Amasa Walker

  
  Francis Amasa Walker (July 2, 1840 – January 5, 1897) was an American economist, statistician, journalist, educator, academic administrator, and an officer in the Union Army.
  
  Walker was born into a prominent Boston family, the son of the economist and politician Amasa Walker, and he graduated from Amherst College at the age of 20. He received a commission to join the 15th Massachusetts Infantry and quickly rose through the ranks as an assistant adjutant general. Walker fought in the Peninsula, Bristoe, Overland, and Richmond-Petersburg Campaigns before being captured by Confederate forces and held at the infamous Libby Prison. In July 1866, he was awarded the honorary grade of brevet brigadier general United States Volunteers, to rank from March 13, 1865, when he was 24 years old. (Full article...)
• 

  

  Kissing circles. Given three mutually tangent circles (black), there are, in general, two possible answers (red) as to what radius a fourth tangent circle can have.

  
  In geometry, Descartes' theorem states that for every four kissing, or mutually tangent circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643.
  
  Frederick Soddy's 1936 poem The Kiss Precise summarizes the theorem in terms of the bends (signed inverse radii) of the four circles: (Full article...)
• 

  

  Three of the ordinary lines in a 4 × 4 grid of points

  
  The Sylvester–Gallai theorem in geometry states that every finite set of points in the Euclidean plane has a line that passes through exactly two of the points or a line that passes through all of them. It is named after James Joseph Sylvester, who posed it as a problem in 1893, and Tibor Gallai, who published one of the first proofs of this theorem in 1944.
  
  A line that contains exactly two of a set of points is known as an ordinary line. Another way of stating the theorem is that every finite set of points that is not collinear has an ordinary line. According to a strengthening of the theorem, every finite point set (not all on one line) has at least a linear number of ordinary lines. An algorithm can find an ordinary line in a set of $n$ points in time $O(n\log n)$. (Full article...)
• 

  

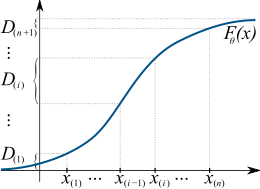
  The maximum spacing method tries to find a distribution function such that the spacings, D_(i), are all approximately of the same length. This is done by maximizing their geometric mean.

  
  
  In statistics, maximum spacing estimation (MSE or MSP), or maximum product of spacing estimation (MPS), is a method for estimating the parameters of a univariate statistical model. The method requires maximization of the geometric mean of spacings in the data, which are the differences between the values of the cumulative distribution function at neighbouring data points.
  
  The concept underlying the method is based on the probability integral transform, in that a set of independent random samples derived from any random variable should on average be uniformly distributed with respect to the cumulative distribution function of the random variable. The MPS method chooses the parameter values that make the observed data as uniform as possible, according to a specific quantitative measure of uniformity. (Full article...)

Did you know

• ... that The Math Myth advocates for American high schools to stop requiring advanced algebra?
• ... that after Archimedes first defined convex curves, mathematicians lost interest in their analysis until the 19th century, more than two millennia later?
• ... that circle packings in the form of a Doyle spiral were used to model plant growth long before their mathematical investigation by Doyle?
• ... that Kit Nascimento, a spokesperson for the government of Guyana during the aftermath of Jonestown, disagrees with current proposals to open the former Jonestown site as a tourist attraction?
• ... that the British National Hospital Service Reserve trained volunteers to carry out first aid in the aftermath of a nuclear or chemical attack?
• ... that people in Madagascar perform algebra on tree seeds in order to tell the future?
• ... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
• ... that the word algebra is derived from an Arabic term for the surgical treatment of bonesetting?

Did you know...

• ...that a cyclic cellular automaton is a system of simple mathematical rules that can generate complex patterns mixing random chaos, blocks of color, and spirals?
• ...that a nonconvex polygon with three convex vertices is called a pseudotriangle?
• ...that the axiom of choice is logically independent of the other axioms of Zermelo–Fraenkel set theory?
• ...that the Pythagorean Theorem generalizes to any three similar shapes on the three sides of a right-angled triangle?
• ...that the orthocenter, circumcenter, centroid and the centre of the nine-point circle all lie on one line, the Euler line?
• ...that an arbitrary quadrilateral will tessellate?
• ...that it has not been proven whether or not every even integer greater than two can be expressed as the sum of two primes?

Featured pictures

• 
  Mandelbrot set, start, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Fields Medal, back, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
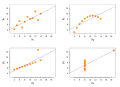
  Anscombe's quartet, by Schutz (edited by Avenue) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 4, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Hypotrochoid, by Sam Derbyshire (edited by Anevrisme and Perhelion) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Line integral of scalar field, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 8, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 7, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 5, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Lyapunov fractal, by BernardH (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 9, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 3, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 13, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 1, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 14, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Cellular automata at Reflector (cellular automaton), by Simpsons contributor (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Missing square puzzle, by Fibonacci (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 2, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
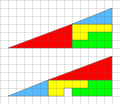
  Proof of the Pythagorean theorem, by Joaquim Alves Gaspar (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 11, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Fields Medal, front, by Stefan Zachow (edited by King of Hearts) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Radian, by Lucas V. Barbosa (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 10, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 6, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Breeder, by Protious/Hyperdeath (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Lorenz attractor at Chaos theory, by Wikimol (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Non-uniform rational B-spline, by Greg L (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbulb, by Ondřej Karlík (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Mandelbrot set, step 12, by Wolfgangbeyer (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Helicatenoid, by Wickerprints (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Desargues' theorem, by Dynablast (edited by Jujutacular and Julia W) (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Tetrahedral group at Symmetry group, by Debivort (from Wikipedia:Featured pictures/Sciences/Mathematics)
• 
  Topological knots, by Jkasd (from Wikipedia:Featured pictures/Sciences/Mathematics)

Get involved

For editor resources and to collaborate with other editors on improving Wikipedia's Mathematics-related articles, visit WikiProject Mathematics.

Categories

» Category:Mathematics, Category:People

Topics

» Lists of mathematics topics, Glossary of areas of mathematics, History of mathematics

Index of articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Vital articles

» subpages: Level 4 Mathematics articles, Level 5 Mathematics articles

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals